2 ABM in archaeology
ABM has conceptual roots and applications in other fields dating back to the early days of computer science. However, this methodology took its current form and was introduced more broadly into the social sciences only in the 1990s.
ABM has been exceptionally well accepted by archaeologists, given its pre-adaptation to distributed and stochastic processes. Most phenomena of interest for archaeology can be represented with ABM, to the satisfaction of archaeologists. Other modelling and simulation approaches (e.g., Dynamic Systems) were, and still are, used but often encounter strong resistance because of their higher abstraction and simplification.
2.1 A transdisciplinary approach
ABM flexibility is also highly valued by researchers in archaeology, given that it is a discipline both historically and thematically positioned between other disciplines at the overlap of the so-called natural and artificial worlds. An ABM model can handle multiple layers of entities and relationships, allowing it to integrate entire models under the same hood.
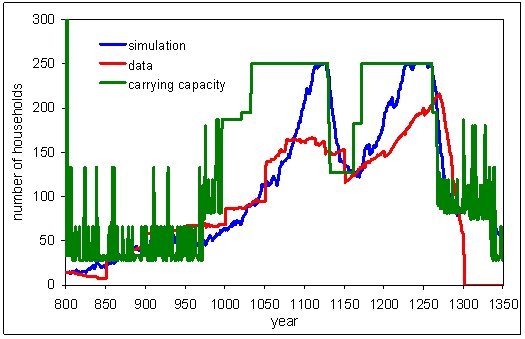
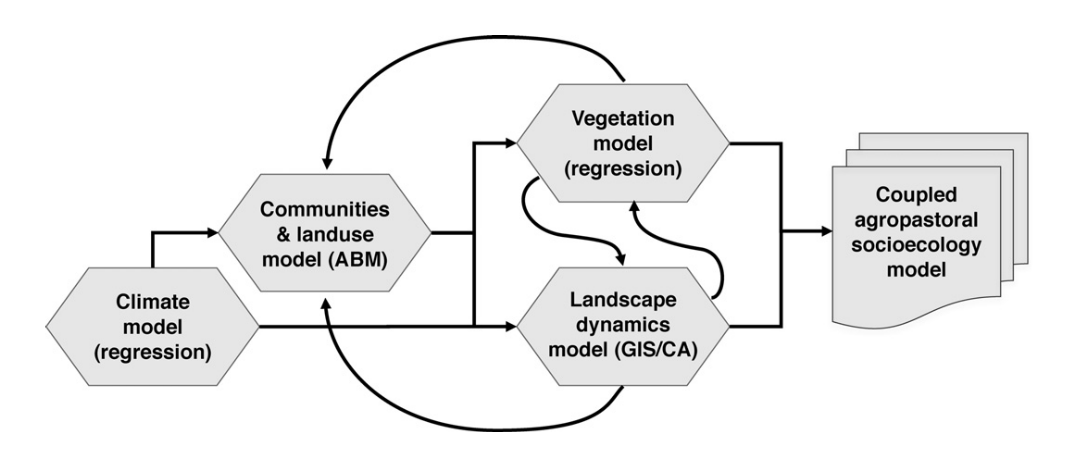
Disciplines such as ecology, environmental science, and geography have exploited the same advantage. This approach has driven the development of models in archaeology for more than two decades. Some authors have called this transdisciplinary framework the research of socio-ecological systems (SES), which has been defined in close relation to the broader complexity science approach. One of the first public successes of ABM in archaeology, the model known as the Artificial Anasazi model (Axtell et al. 2002), emerged from this approach as a collaboration among researchers orbiting the Santa Fe Institute.
Despite its positive influence in pushing the field forward, the SES approach has also limited the diversity of scope and theory used with ABM in archaeology. ABM under SES aligns particularly well, for example, with research questions related to landscape and environmental archaeology and formulated from a processualist perspective. This tutorial is no exception. To the potential “new blood” in this field, I recommend keeping your mind open to all questions and theoretical frameworks, especially those you are already invested in.
ABM in archaeology has been a prolific field, though it remains a small community. Here, we will only cover a small part of the field, specifically from my perspective. For a broader introduction to the many contributions in this field, I refer you to any of the introductions in the References. I recommend the recent textbook by Romanowska, Wren & Crabtree (2021), which also includes many practical exercises in NetLogo, using a programming style and philosophy that differ significantly from this tutorial.
2.2 Domains of application and examples
Here is a non-exhaustive list of examples of simulation and ABM in archaeology organised by topics:
- Physico-chemical dynamics
- Artefact production: operational chain (chaîne opératóire), authorship and style, material transformations during manufacturing (Sorensen and Scherjon 2018), use and deposition (Gravel-Miguel and Wren 2018).
- Site formation: distribution of artefacts and structures (Gravel-Miguel and Wren 2018), preservation, strata formation and taphonomy (Davies et al. 2016), sample bias.
- Artefact production: operational chain (chaîne opératóire), authorship and style, material transformations during manufacturing (Sorensen and Scherjon 2018), use and deposition (Gravel-Miguel and Wren 2018).
- Ecological dynamics
- Climate patterns: seasonality (Angourakis, Bates, et al. 2022), regional variations, climate change (Bocquet-Appel et al. 2014).
- Soils: erosion and sediment accumulation (Kabora et al. 2020; Robinson et al. 2018; Ullah et al. 2019).
- Hydrological dynamics: water availability, run-off, irrigation (Altaweel and C. Watanabe 2012; Altaweel and C. E. Watanabe 2012).
- Vegetation: plant domestication (Angourakis, Alcaina-Mateos, et al. 2022), crop dynamics (Angourakis, Bates, et al. 2022; Baum et al. 2016; Boogers and Daems 2022; Christiansen and Altaweel 2006; Joyce 2019; Robinson et al. 2018), deforestation and fires (Boogers and Daems 2022; Nikulina et al. 2024; Snitker 2021, 2018).
- Non-human animal behaviour: dynamics of wild populations under human influence (Morrison and Allen 2017), domestic animal population dynamics (Günther et al. 2021), herd behaviour, animal husbandry, transhumance (Günther et al. 2021) (See also the Dairy-versus-Transhumance model, my own work, still under development).
- Climate patterns: seasonality (Angourakis, Bates, et al. 2022), regional variations, climate change (Bocquet-Appel et al. 2014).
- Anthropological dynamics
- Individuals: pedestrian dynamics (Lake 2001), foraging (Brantingham 2006; Oestmo et al. 2016), metabolism, kinship (Rogers 2013), health and population dynamics (mating and marriage, reproduction, mortality) (Verhagen 2019), cognition (memory, rationality and learning) (Mokom 2015; Premo and Tostevin 2016; Sousa et al. 2019; Acerbi et al. 2020), individual-to-individual cooperation and competition (Graham 2009; Sousa et al. 2019; White 2013).
- Groups: household organization and microeconomics (Christiansen and Altaweel 2006; Joyce 2019), emergence of alliances and organisations (Cioffi-Revilla et al. 2015; White 2013), group-to-group cooperation and competition (Angourakis et al. 2014, 2015, 2017; Cioffi-Revilla et al. 2015; Rogers 2013), group mobility (Rogers 2013; Santos et al. 2015), logistics and military tactics (Rubio Campillo et al. 2012; Rubio-Campillo et al. 2014; Verhagen 2019), prestige, reward and punishment, social learning, cultural transmission and norm emergence (Gower-Winter 2022; Mokom 2015; Premo and Tostevin 2016; Drost and Vander Linden 2018; Acerbi et al. 2020).
- Settlements: population dynamics (Verhagen 2019; Crema 2014), resource exploitation (Boogers and Daems 2022), trade (Carrignon et al. 2020; Chliaoutakis and Chalkiadakis 2020; Lawall and Graham 2018; Ortega et al. 2014; Sakahira et al. 2021), migration, macro-economics, urbanisation, cultural evolution (Carrignon et al. 2020; Gower-Winter 2022; Lake and Crema 2012; Mokom 2015; Sakahira et al. 2021), settlement patterns and land use (Altaweel et al. 2015; Chliaoutakis and Chalkiadakis 2020; Angourakis et al. 2014, 2017; Boogers and Daems 2022; Joyce 2019; Robinson et al. 2018; Rogers 2013; Snitker 2018; Ullah et al. 2019), politogenesis (Cioffi-Revilla et al. 2015; Rogers 2013; Turchin 2018), catastrophic collapse or abandonment (Kohler and Varien 2012; McAnany et al. 2015).
- Regional to global: cooperation and competition between territorial states (Turchin 2018), trade routes (Chliaoutakis and Chalkiadakis 2020; Lawall and Graham 2018; Ortega et al. 2014), human species dispersal (Callegari et al. 2013) and genetic and cultural diffusions (Bocquet-Appel et al. 2014; Kovacevic et al. 2015; Mokom 2015)
2.3 Examples
- “Artificial Anasazi” (Axtell et al. 2002; Janssen 2009)
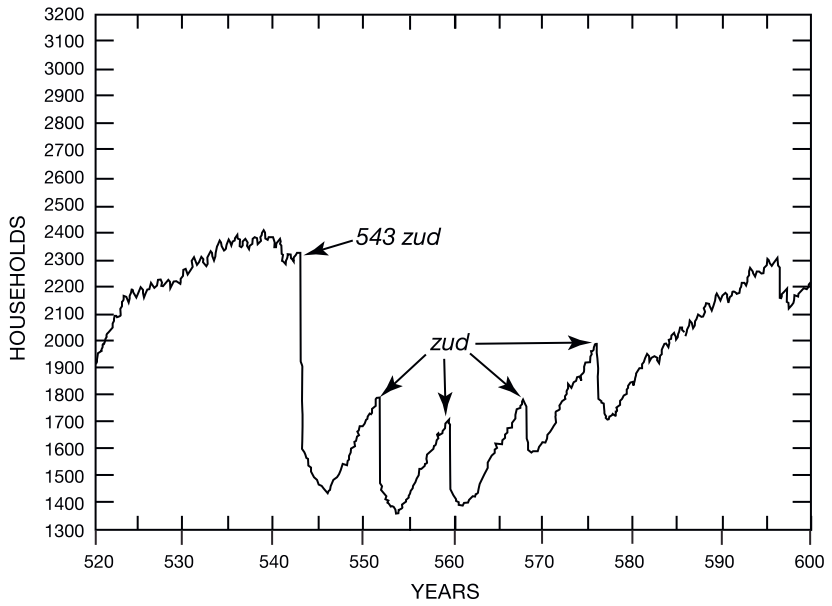
The Artificial Anasazi model was developed to explore population dynamics in Long House Valley, Arizona. The model represents a population of households, with a simplified food economy based on maize cultivation. By simulating this system, researchers tested the hypothesis that climate change was the main cause of the valley’s abandonment.
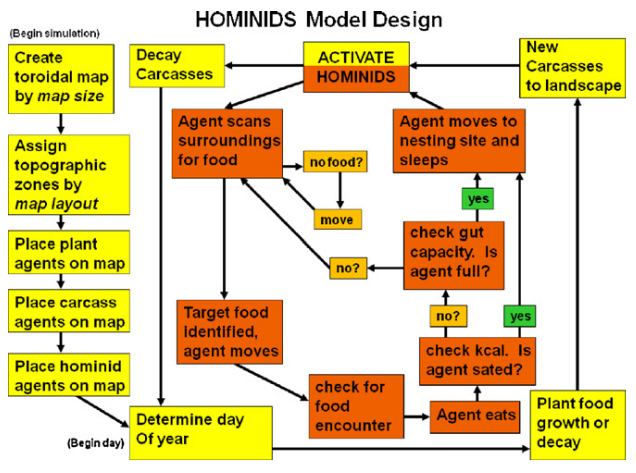
- “HOMINIDS” (Griffith et al. 2010)
- “MedLanD” (Barton et al. 2012)
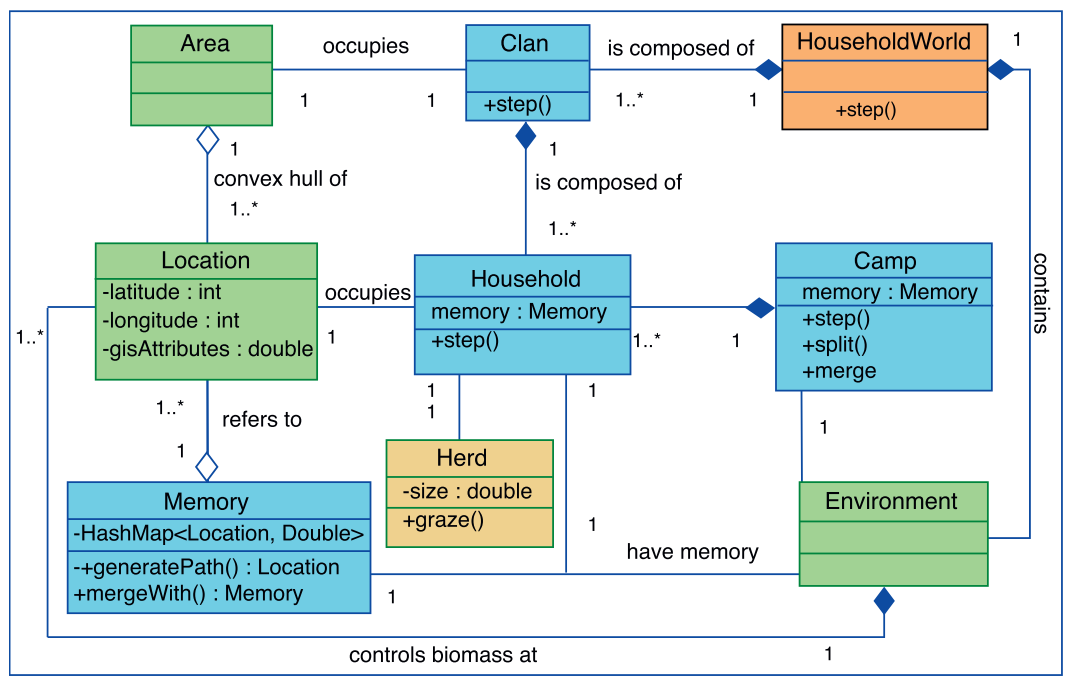
- “HouseholdsWorld” (Rogers et al. 2012)
- MayaSim (Heckbert 2013)
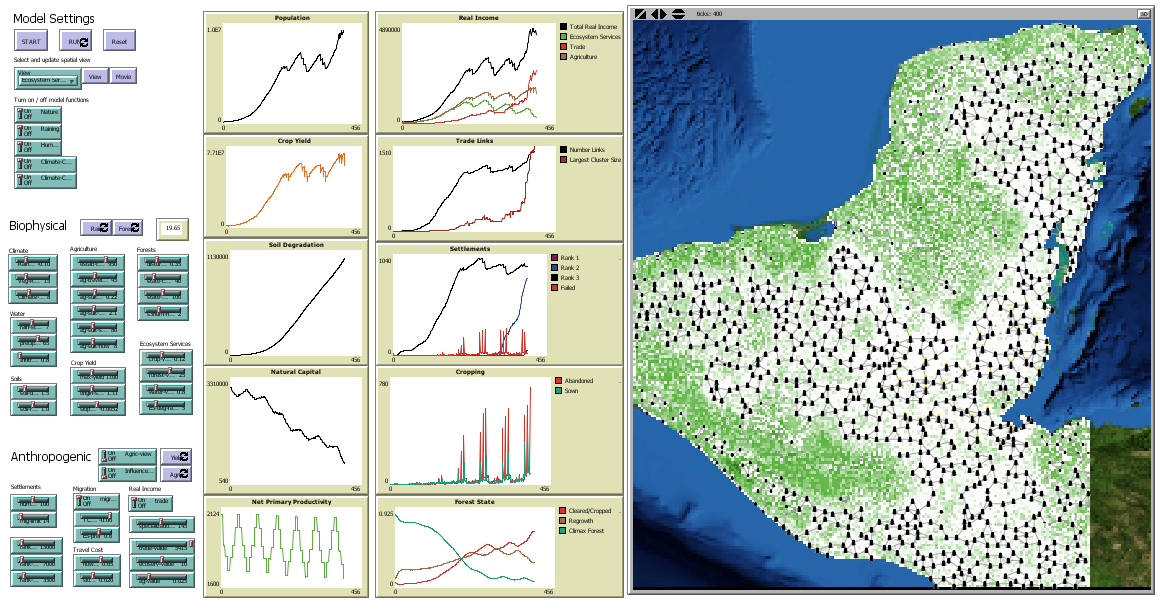
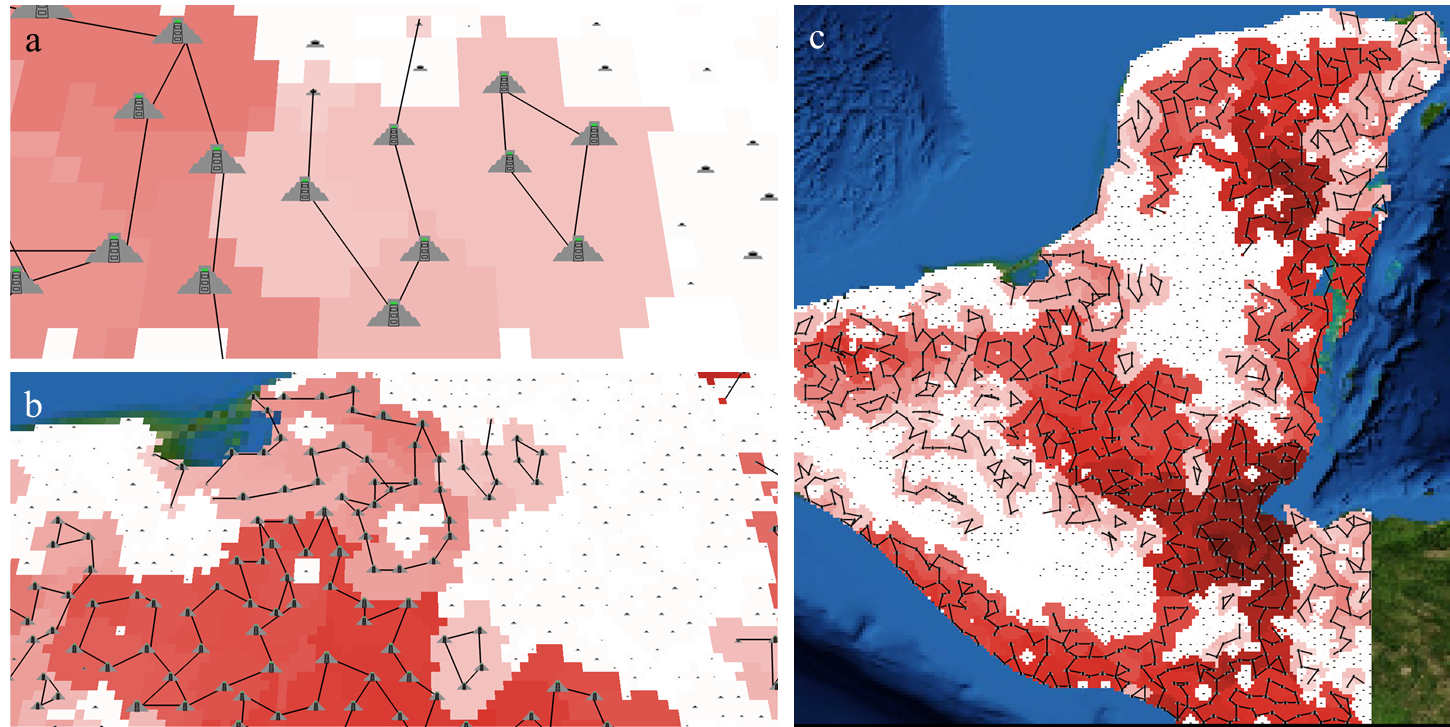
- “Indus Village” (Angourakis 2021; Angourakis et al. 2020, 2025; Angourakis, Bates, et al. 2022)
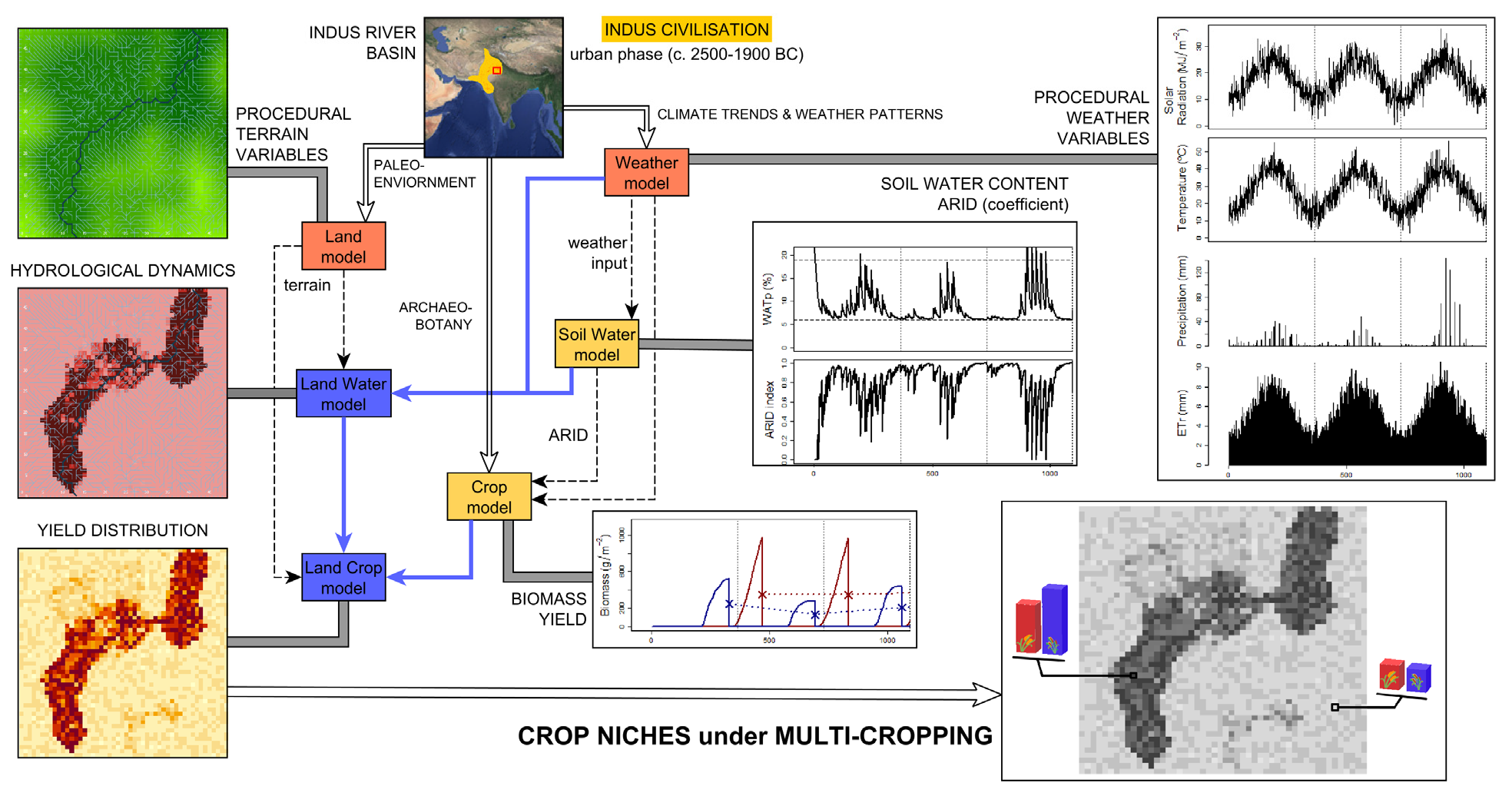
repository: https://github.com/Andros-Spica/indus-village-model
2.4 Unfinished business: representation and validation
Despite the relative success and proliferation of agent-based modelling in archaeology, an unsolved debate remains over the epistemological nature of simulation models as explanatory.
To be explanatory, models must connect a process to a phenomenon, as defined to the best of our knowledge (representation), and to the evidence we raise and select as relevant (validation). Both archaeologists and non-simulation modellers sometimes dismiss agent-based models in archaeology as straying too far from archaeological evidence. Why should we dare (or even bother) to simulate past processes that cannot be observed through material remains?
Unfortunately, it is too easy to ignore the difference between descriptive and explicative models and leave archaeological interpretations imposed on descriptive models unchecked by formalisation. When a descriptive mathematical model is used, a good validation result (fit given an evidence set) does not guarantee that the interpretative model represents the process to which it is attributed. More importantly, good validation can be mistaken for good representation.
For example, imagine we, as archaeologists, are convinced that humans could feed on a certain kind of rock at some remote point in the past. When we apply the most robust methods in cartography and inferential statistics to evidence of human presence and findings of such rocks, we might find that a positive correlation confirms our belief. However, the representational link between our interpretation and the reality of the past process is weak. Our belief would hold only if it were impermeable to formalisation and a broader knowledge base. Alternatively, perhaps, we would quickly realise the metabolic constraints of stone digestion.
Modelling structures your thoughts about the world, and mathematical modelling does so with extra discipline. Explanatory and, particularly, simulation modelling, however, is doing that specifically for reconstructing processes, stories, or, in other words, the mechanisms or webs of causality that we presume to be behind the semi-static reality we observe (e.g., archaeological materials).
Non-simulation computational modelling in archaeological research 
Simulation modelling in archaeological research 
We will practice distinguishing between phenomena, evidence, and mechanism when designing our own conceptual model.